In this article we will describe the algorithm we submitted to the Helsinki Tomography Challenge 2022. The purpose of the challenge is to recover the shapes of 2D targets imaged with limited-angle tomography. The task is challenging because there is not enough data for standard algorithms to reconstruct properly, so one needs to come up with a better plan.
The training set of the HTC2022 challenge consist of homogenous acrylic disc phantoms of 70 mm in diameter, with holes of varying shapes made with a laser cutter. Each disk has a different number of irregular holes in random locations.
Figure 1: the training set of the HTC2022 challenge.
In the figure below, we show the reconstruction with the standard FDK algorithm of the training sample A, on the left with the full angular range, and on the right the limited angle counterpart, covering only 1/12 of the whole angular range, i.e. 30 degrees.
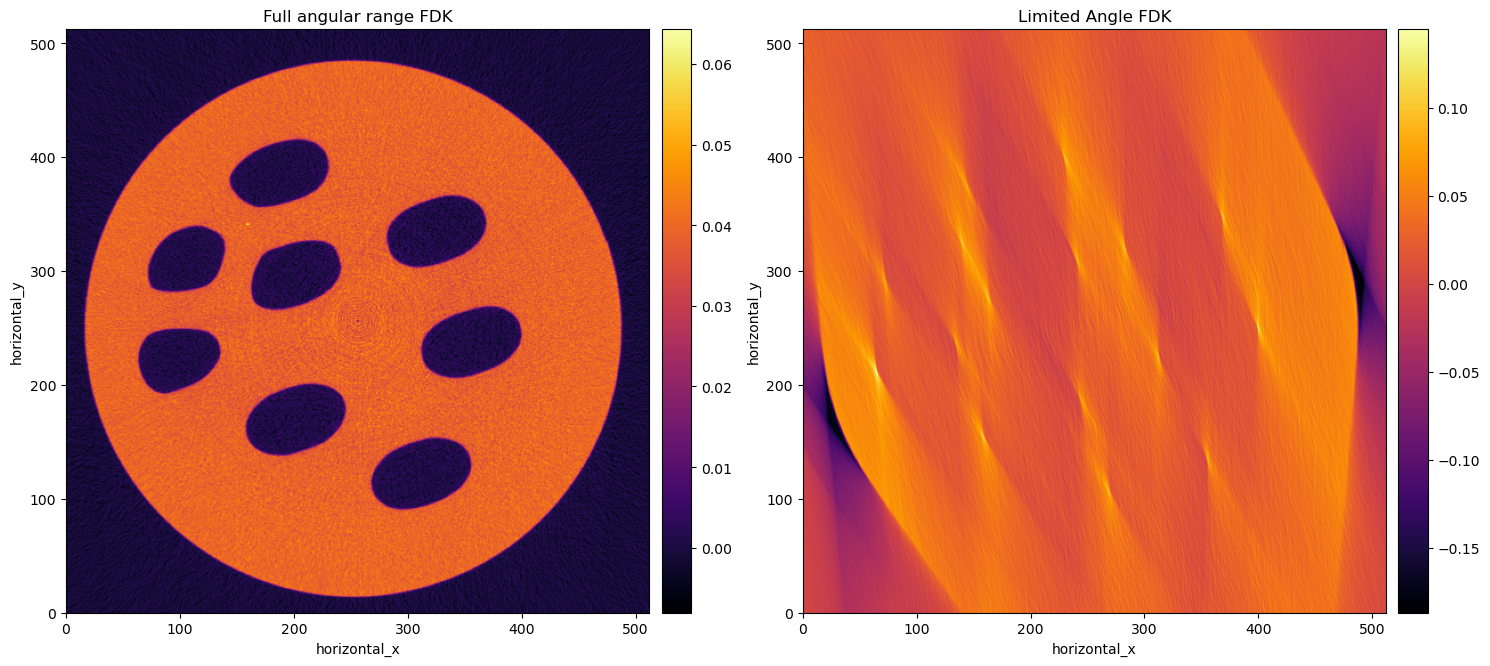
One of the limits of the FDK algorithm is that it requires full angular coverage. FDK clearly cannot cope with the missing information, so we will use an iterative method which does not require, by definition, the full angular coverage. Using CIL, we set up an optimisation problem trying to find a solution which minimises the least squares (LS) function between our acquired data and the ones coming from our solution. (Please check our paper for a detailed description on how this is possible).
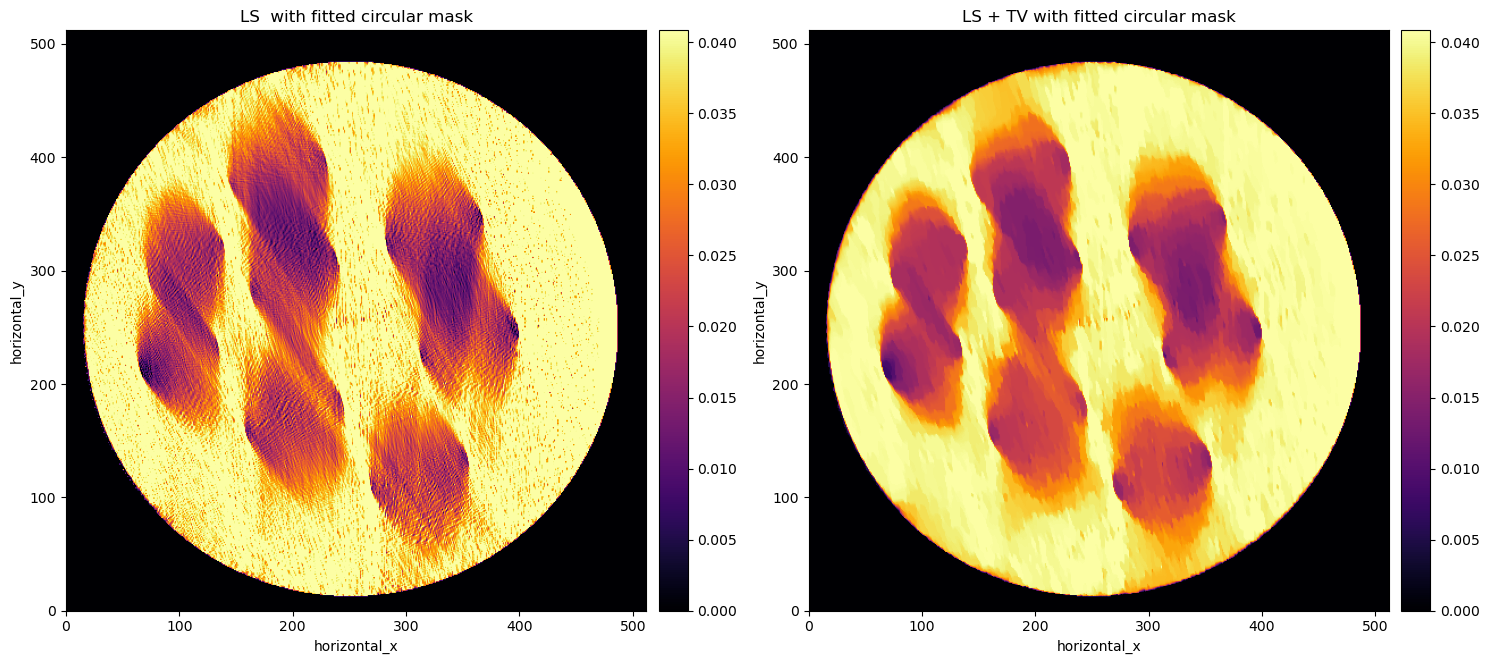
In the image below, we see the LS reconstruction on the left. Clearly just an iterative algorithm isn’t sufficient for limited angle data. But with an iterative algorithm one can add some prior knowledge to help the algorithm find the right solution. In this case we know that there is only a single homogeneous material, so adding a Total Variation (TV) regulariser may help. In fact TV favours homogeneous regions with sharp boundaries.
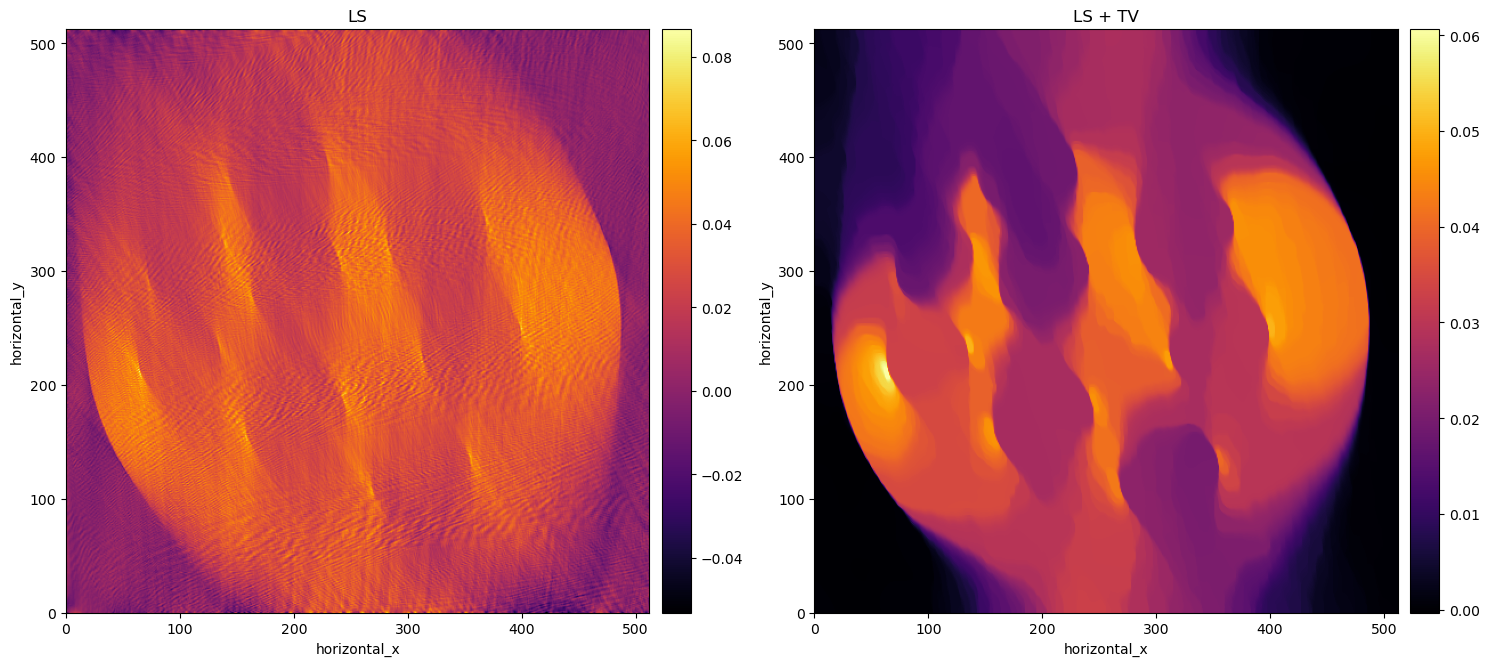
The addition of TV made a huge difference with respect to the sole LS data fitting term, however the reconstruction is particularly poor where there is no data, i.e. top-left bottom-right.
We know that there is only one uniform material in the scan and we know its absorption coefficient. So we can enforce a limit to the reconstruction to that value and furthermore, we can add TV regularisation. We see the effect of this constraint added to LS and LS + TV in the image below.
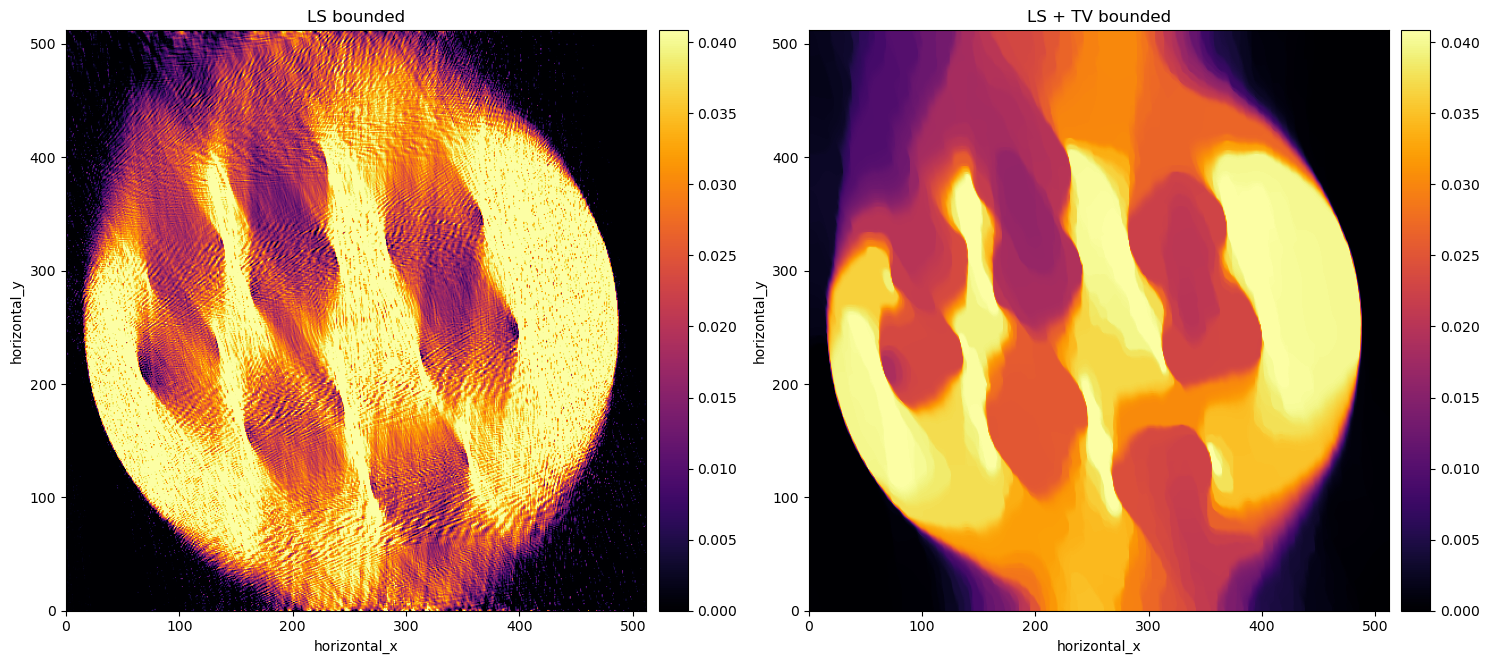
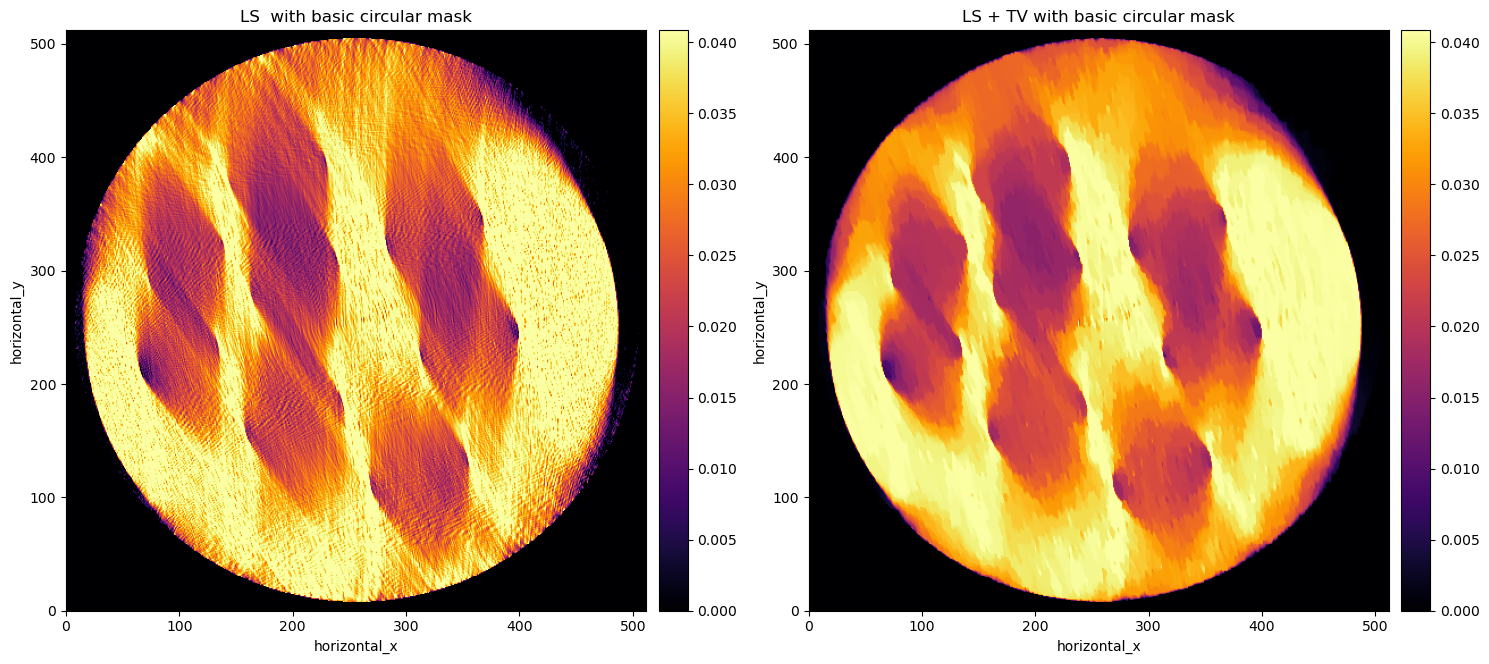
Another step in the right direction, but now we can notice that the real object really is within a smaller circle, i.e. our mask is slightly too large! Therefore, we developed a method to fit a circle to the sharp edges of the reconstruction that are visible on the top-right bottom-left of the original FDK reconstruction. The final reconstruction is in the following plot.
In the assessment of the algorithm performance the judges will look at a segmentation of the reconstruction into two components: air and plastic. This segmentation is scored against a segmentation obtained with a full angle coverage dataset.

